• XAVIER VIENNOT
  • Foreword
    • Preface
    • Introduction
    • Acknowledgements
    • Lectures for wide audience
  • PART I
    • Preface
    • Abstract
    • Contents
    • Ch0 Introduction to the course
    • Ch1 Ordinary generating functions
    • Ch2 The Catalan garden
    • Ch3 Exponential structures and genarating functions
    • Ch4 The n! garden
    • Ch5 Tilings, determinants and non-intersecting paths
    • Lectures related to the course
    • List of bijections
    • Index
  • PART II
    • Preface
    • Abstract
    • Contents
    • Ch1 Commutations and heaps of pieces: basic definitions
    • Ch2 Generating functions of heaps of pieces
    • Ch3 Heaps and paths, flows and rearrangements monoids
    • Ch4 Linear algebra revisited with heaps of pieces
    • Ch5 Heaps and algebraic graph theory
    • Ch6 Heaps and Coxeter groups
    • Ch7 Heaps in statistical mechanics
    • Lectures related to the course
  • PART III
    • Preface
    • Abstract
    • Contents
    • Ch0 overview of the course
    • Ch1 RSK The Robinson-Schensted-Knuth correspondence
    • Ch2 Quadratic algebra, Q-tableaux and planar automata
    • Ch3 Tableaux for the PASEP quadratic algebra
    • Ch4 Trees and tableaux
    • Ch5 Tableaux and orthogonal polynomials
    • Ch6 Extensions: tableaux for the 2-PASEP quadratic algebra
    • Lectures related to the course
    • References, comments and historical notes
  • PART IV
    • Preface
    • Introduction
    • Contents
    • Ch0 Overview of the course
    • Ch1 Paths and moments
    • Ch2 Moments and histories
    • Ch3 Continued fractions
    • Ch4 Computation of the coefficients b(k) lambda(k)
    • Ch5 Orthogonality and exponential structures
    • Ch6 q-analogues
    • Lectures related to the course
    • Complements
    • References
  • Epilogue

The Art of Bijective Combinatorics    Part II
Commutations and heaps of pieces
with interactions in physics, mathematics and computer science

The Institute of Mathematical Sciences, Chennai, India  (January-March 2017)

Preface

This is Part II of the so-called "video-book" "The Art of Bijective Combinatorics" ("ABjC" for short). It is based on a course given in 2017 at The Institute of Mathematical Science (IMSc), Chennai, India, at the invitation of Amritanshu Prasad (Amri).
Analogously to the other Parts of ABjC, there are 3 components:
- a set of 19 lectures video-recorded available on YouTube, Ekalavya  (the IMSc Media Center in India) and the Chinese chain bilibili
- the corresponding set of slides of each lecture,
- this website which enable one to navigate inside the videos, in the same way you turn around the pages of a book. For example if you click on the time given just after the slide number corresponding to one of the videos, you will get, up to one second, to exact position in the video.

The  playlist from matsciencechannel of the 19 videos of this course is here

In 1969 P. Cartier and D.Foata introduced the "commutation monoids", that is monoids of words defined up to a certain commutation of letters, in the monograph:
 P. Cartier and D. Foata, Problèmes combinatoires de commutation et réarrangements, Lecture Notes in Mathematics, no. 85, Springer–Verlag, Berlin, New York, 1969.
In 1985 the author introduced the notion of "heaps of pieces", as a geometric interpretation of these "commutation monoids". This interpretation is based on a powerful spatial intuition, which is missing in the vision with words, up to some commutation of letters, of the Cartier-Foata monoid. Of course everything written in terms of commutation monoids can be written in terms of heaps.
The paper is: G.X.V., Heaps of pieces. I. Basic definitions and combinatorial lemmas, in Combinatoire énumérative (Montréal, Québec,1985), vol. 1234 of Lecture Notes in Math., pp321–350, Springer, Berlin, 1986.

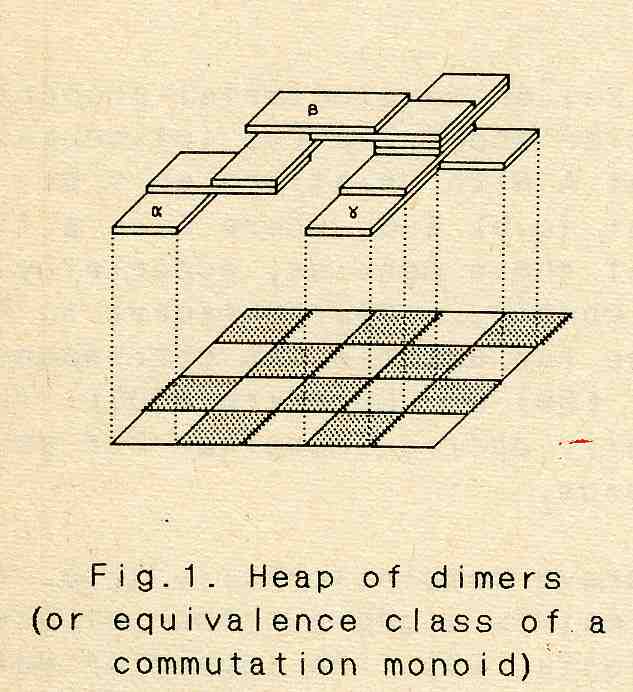
Some Figures
from the paper
Heaps of pieces I
 in Combinatoire
énumérative,
Montréal,
Québec  1985
LN in Maths n°1234

 In this paper, the author announce several papers in preparation (Heaps of pieces II, ..., V), papers which ... have never been written. Meanwhile the monograph of Cartier and Foata has been republished in the "books" section of the Séminaire Lotharingien de Combinatoire and an appendix was added in 2006 by C. Krattenthaler, The theory of heaps and the Cartier-Foata monoid.
A companion paper to the 1986 paper Heaps of pieces. I. Basic definitions and combinatorial lemmas, is the following:
G.  Viennot, Problèmes  combinatoires  posés  par  la  physique  statistique,  Astérisque,  SMF,  tome  121–122  (1985),  Séminaire Bourbaki, 36ème année 1983/84, exposé 626, Feb 1984, p225–246.    Available here on Numdam .
It is the purpose of this course to complete the gap from the original 1985 and 1986 papers, together with the exposition of many results and works which have been done since this paper, with connections and applications to physics (statistical mechanics, quantum gravity), computer science (Petri nets, asynchronous automata) and other parts of mathematics (orthogonal polynomials, totally commutative elements in Coxeter groups, chromatic polynomials and zeta function of graphs, Lie algebras, etc). The heaps methodology appears to be popular, as show by some recent (2020-21) work.
For example, we just quote 7 recent papers written in 2020-21 where heaps plays a central role:
- Tyler Helmuth and Assaf Shapira, Loop-erased random walk as a spin system observable, (17pp) arXiv:2003:19928v2 [matrh.PR] Aug 2020
- A.M. Garsia and G. Ganzberger, Fibonacci polynomials, (18 pp) arXiv:2009.10213 [math.CO] Sep 2020.
- M.V. Tamm, N. Pospelov and S. Nechaev, Growth rate of 3D heaps of pieces, (14pp) arXiv: 2009.12540v2 [cond-math.stat-mech]  Oct 2020
- P.-L. Giscard, Counting walks by their last erased self-avoiding polygons using sieves, (48pp) arXiv: 2001.02084 [math.CO] Nov 2020
- E. Bagno, R. Biagioli, F. Jouhet and Y. Roichman, Block number, descents and Schur positivity of fully commutative elements in B_n, (25 pp)
arXiv:2012.06412 [math.CO] Dec 2020.
- J. Cigler and C. Krattenthaler, Bounded Dyck paths, bounded alternating sequences, orthogonal polynomials, and reciprocity, (70 pp) arXiv:2012.03878 [math.CO] Dec 2020.
- L. Fredes, J.-F. Marckert, Aldous-Broder theorem: extension to the non reversible case and new combinatorial proof, (18 pp) arXiv: 2102.08639 [math.CO] Feb 2021
together with a chapter of the book (Lecture 4, Heaps, Continued Fractions and Orthogonal Polynomials, pp 97-135):
- A. M. Garsia and Ö. E ̆gecio ̆glu, Lectures in Algebraic Combinatorics, Lecture Notes in Math, vol 2277, Springer, Cham, 2020.
A course at two different levels
 I gave this course at two different levels at the same time. Most of the courses are supposed to be followed by good undergraduate students (at the Master level) and graduate students. I also gave some more advanced topics, opening some «windows» without proof, for graduate students, researchers and professors, in connection with active researches in combinatorics, and sometimes with connection in theoretical physics and computer science. Such sections are listed under the name «Complements». 
How to quote this video-book in the literature
The videos, slides and the address of this video-book ABjC will remain unchanged. It is possible to quote this video-book in the literature in the same way as quoting a book.  If you give only the direct link to a set of slides, or to the YouTube address of a video, the reader will miss the corresponding page giving the precise description of the slides, video and direct links in order to navigate inside the video. Also think of our Chinese colleagues, for which the link to the video is only through the popular Chinese chain "bilibili". 
I suggest the following:
-     if you want to quote this volume of ABjC, I suggest to quote in an analogous way to a book, with the editor (here IMSc), the place of edition (here Chennai) and the year (here 2017), for example:
The Art of Bijective Combinatorics, Part II, Commutations and heaps of pieces, IMSc, Chennai, 2017, http://www.viennot.org/abjc2.html
 the pointer is going to this web page (Preface of Part II of ABjC)
-     if you want to quote a precise point inside the video-book, as for example a definition, theorem or bijection, I suggest to refer to the number(s) of the corresponding slide(s). Example:  if you want to quote "1995 Stembridge’s characterization of fully commutative heaps" from Chapter 6a:
The Art of Bijective Combinatorics, Part II, Commutations and heaps of pieces, Chapter  6a, IMSc, Chennai, 2017, p43, http://www.viennot.org/abjc2-ch6.html
the suffix abjc2-ch6.html refers to the web page dedicated to Chapter 6 of Part "II" of ABjC, this page contains the different slides and videos of the two corresponding lectures Ch6a, Ch6b. In front of slide 43 of Chapter 6a the reader will find the link  38:06 going directly to the YouTube video at slide 43.
 -     if you want to quote the whole collection of the 4 volumes then:
The Art of Bijective Combinatorics, IMSc, Chennai, 2016-2019, http://www.viennot.org/abjc.html
the suffix /abjc.html refers to the web page of the (general) preface of ABjC.
Xavier Viennot
email: first name (at) name (dot) org